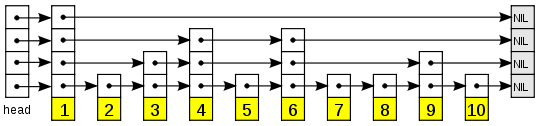
The skip list is a relative unknown data structure. If you know it already you can stop reading. If not, keep reading because “the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.” (William Pugh) [Skip lists: a probabilistic alternative to balanced trees]. Speaking from experience, I have to say this is true. Coding up skip lists is easy. I’ve written a reentrant version that uses read/write locking, a version for a hash table to replace chaining, a version that allows Θ(log(n)) indexing, and an unrolled version. It is not perfect for all problems, but it is adaptable and has some other nice properties. However, I like it best for its simplicity. To find the 7 in the above skip list, we start at the top left, and go right until we hit a value >7 (or NIL). We go down one and continue to the right, and so on. So we visit the nodes 1, 4, 6, and 7. Search usually is Θ(log(n)). Since the reentrant version is somewhat less trivial to write, click this link for a GPLed implementation.
